Aprendiendo Geometría Analítica
GEOMETRÍA ANALÍTICA
La geometría analítica es una rama de las matemáticas que estudia con profundidad las figuras, sus distancias, sus áreas, puntos de intersección, ángulos de inclinación, puntos de división, volúmenes, etc. Es un estudio más profundo para saber con detalle todos los datos que tienen las figuras geométricas.Estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, continúa con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica.
Actualmente, la geometría analítica tiene múltiples aplicaciones, más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.
A) Ecuación de la recta
1. Ecuación general de la recta:
Esta es una de las formas de representar la ecuación de la recta.
De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano) , con abscisas (x) y ordenadas (y) .
| Recuerden que es imprescindible dominar todos los aspectos sobre el Plano cartesiano pues la Ecuación de la recta no tiene existencia conceptual sin un Plano cartesiano. |
Ahora bien, conocidos esos dos puntos, todas las rectas del plano, sin excepción, quedan incluidas en la ecuación
Ax + By + C = 0
Que también puede escribirse como
ax + by + c = 0
y que se conoce como: la ecuación general de la línea recta, como lo afirma el siguiente:
Teorema
La ecuación general de primer grado Ax + By + C = 0 , donde A, B, C pertenecen a los números reales (
|
2.– Ecuación ordinaria de la recta:
Esta es otra de las formas de representar la ecuación de la recta.
Pero antes de entrar en la ecuación principal de la recta conviene recordar lo siguiente:
Cada punto (x, y) que pertenece a una recta se puede representar en un sistema de coordenadas, siendo x el valor de la abscisa (horizontal) e y el valor de la ordenada (vertical).
(x, y) = (Abscisa , Ordenada)
Ejemplo: El punto (–3, 5) tiene por abscisa –3 y por ordenada 5.
Si un par de valores (x, y) pertenece a la recta, se dice que ese punto satisface la ecuación.
Ejemplo: El punto ( 7, 2 ) (el 7 en la abscisa x y el 2 en la ordenada y ) satisface la ecuación y = x – 5 , ya que al reemplazar queda
2 = 7 – 5 lo que resulta verdadero.
Recordado lo anterior, veamos ahora la ecuación de la recta que pasa solo por un punto conocido y cuya pendiente (de la recta) también se conoce , que se obtiene con la fórmula
y = mx + n
que considera las siguientes variables: un punto ( x, y ), la pendiente ( m ) y el punto de intercepción en la ordenada ( n ), y es conocida como ecuación principal de la recta (conocida también como forma simplificada, como veremos luego).
3. Forma simplificada de la ecuación de la recta:
Si se conoce la pendiente m , y el punto donde la recta corta al eje de ordenadas es ( 0, b ) (corresponde a n en la fórmula principal ya vista), podemos deducir, partiendo de la ecuación de la recta de la forma
y − y 1 = m(x − x 1 )
y – b = m(x – 0)
y – b = mx
y = mx + b
Esta es una segunda forma de la ecuación principal de la recta (se la llama también forma explícita de la ecuación ) y se utiliza cuando se conocen la pendiente y la ordenada al origen (o intercepto), que llamaremos b ( no olvidemos que corresponde a la n en la primera forma de la ecuación principal). También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.
Ejemplo: La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo cual indica que interceptará al eje y en el punto (0, 7) .
Conocida la fórmula de la ecuación principal (simplificada o explícita, como quieran llamarla) de la recta es posible obtener la ecuación de cualquier recta siempre que se nos den al menos dos variables de ella: puede ser la pendiente, puede ser un punto o puede ser el intercepto.
Esto significa que si te dan esa información se puede conseguir una ecuación de la forma y = mx + b que cumple con esas condiciones dadas. Nótese que la ecuación y = mx + b es la forma generalizada de la forma principal y = mx + n; por lo tanto, la b corresponde al valor de n (el intercepto en la ordenada y ).
Distancia entre dos puntos |
Por haberlo estudiado, sabemos que el Plano cartesiano se usa como un sistema de referencia para localizar puntos en un plano.
Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x 2 – x 1 ) .
Ejemplo:
La distancia entre los puntos (–4, 0) y (5, 0) es 5 – (–4) = 5 +4 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
Para demostrar esta relación se deben ubicar los puntos P 1 (x 1 , y 1 ) y P 2 (x 2 , y 2 ) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa P 1 P 2 y emplear elTeorema de Pitágoras .
B) Ecuación de la circunferencia
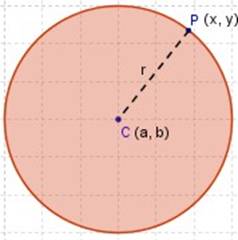
La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro (recordar que estamos hablando del Plano Cartesiano y es respecto a éste que trabajamos).
 |
Una circunferencia queda determinada cuando conocemos:
Tres puntos de la misma, equidistantes del centro.
El centro y el radio.
El centro y un punto en ella.
El centro y una recta tangente a la circunferencia.
1. Ecuación ordinaria:
También podemos decir que la circunferencia es la línea formada por todos los puntos que están a la misma distancia de otro punto, llamado centro .
Esta propiedad es la clave para hallar la expresión analítica de una circunferencia (la ecuación de la circunferencia ).
Entonces, entrando en el terreno de la Geometría Analítica , (dentro del Plano Cartesiano ) diremos que ─para cualquier punto, P (x, y) , de una circunferencia cuyo centro es el punto C (a, b) y con radio r ─, la ecuación ordinaria es
(x ─ a) 2 + (y ─ b) 2 = r 2
2. De la ecuación ordinaria a la ecuación general:
Si en esta ecuación ordinaria ─cuyo primer miembro (lado izquierdo) está formado por la suma de dos cuadrados de binomio─, eliminamos los paréntesis desarrollando dichos binomios, pasamos todos los términos al primer miembro y la igualamos a cero, tendremos:
x 2 ─ 2ax + a 2 + y 2 ─ 2by + b 2 ─ r 2 = 0 ecuación que ordenada sería
x 2 + y 2 ─ 2ax ─ 2by + a 2 + b 2 ─ r 2 = 0
Si para tener una ecuación más sintetizada hacemos las siguientes asignaciones:
─ 2a = D,
─ 2b = E,
a 2 + b 2 ─ r 2 = F
la ecuación quedaría expresada de la forma:
x 2 + y 2 + Dx + Ey + F = 0 conocida como Ecuación General de la Circunferencia, la cual debe cumplir las siguientes condiciones para serlo:
No existe término en xy
Los coeficientes de x 2 e y 2 son iguales.
Si D = ─ 2a entonces 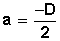 Si E = ─ 2b entonces
Si E = ─ 2b entonces 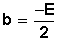 Si F = a 2 + b 2 ─ r 2 entonces
Si F = a 2 + b 2 ─ r 2 entonces 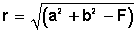 Además, otra condición necesaria para que una ecuación dada represente una circunferencia es que:
Además, otra condición necesaria para que una ecuación dada represente una circunferencia es que:
a 2 + b 2 ─ F > 0 (a 2 + b 2 ─ F debe ser mayor que cero)
Nota:
Para simplificar la ecuación general de la circunferencia (x 2 + y 2 ─ 2ax ─ 2by + a 2 + b 2 ─ r 2 = 0) algunos textos o docentes utilizan otra convención y hacen:
─ 2a = A,
─ 2b = B,
a 2 + b 2 ─ r 2 = C para tener finalmente
x 2 + y 2 + Ax + By + C = 0 que es lo mismo que x 2 + y 2 + Dx + Ey + F = 0
a 2 + b 2 ─ F > 0 (a 2 + b 2 ─ F debe ser mayor que cero)
Nota:

Comentarios
Publicar un comentario